Screw Linear Interpolation

This example shows interpolated trajectories between two random poses.

import matplotlib.pyplot as plt
import numpy as np
import pytransform3d.plot_utils as ppu
import pytransform3d.trajectories as ptr
import pytransform3d.transformations as pt

import jaxtransform3d.transformations as jt

Setup

We generate two random transformation matrices to represent two poses between we want to interpolate. These will also be converted to dual quaternions, exponential coordinates, and position and quaternion.

rng = np.random.default_rng(25)
pose1 = pt.random_transform(rng)
pose2 = pt.random_transform(rng)
dual_quat1 = pt.dual_quaternion_from_transform(pose1)
dual_quat2 = -pt.dual_quaternion_from_transform(pose2)
exp_coords1 = pt.exponential_coordinates_from_transform(pose1)
exp_coords2 = pt.exponential_coordinates_from_transform(pose2)

n_steps = 100

Screw Linear Interpolation between Poses

The ground truth for interpolation of poses is a linear interpolation of rotation about and translation along the screw axis. We will represent the difference between the two poses as exponential coordinates, a product of the screw axis and the magnitude of the transformation. We can use fractions of the exponential coordinates to smoothly interpolate between the two poses.

pose12pose2 = jt.compose_transforms(jt.transform_inverse(pose1), pose2)
exp_coords = pt.exponential_coordinates_from_transform(pose12pose2)
offsets = ptr.transforms_from_exponential_coordinates(
    exp_coords[np.newaxis] * np.linspace(0, 1, n_steps)[:, np.newaxis]
)
interpolated_poses = ptr.concat_many_to_one(offsets, pose1)

Approximation: Linear Interpolation of Dual Quaternions

An approximately correct solution is linear interpolation and subsequent normalization of dual quaternions. The problem with dual quaternions is that they have a double cover and the path of the interpolation might be different depending on which of the two representation of the pose is selected. In this case the path does not match the ground truth path, but when we switch from dq1 to pt.dual_quaternion_double(dq1)—its alternative representation—the interpolation path is very close to the ground truth.

interpolated_dqs = (
    np.linspace(1, 0, n_steps)[:, np.newaxis] * dual_quat1
    + np.linspace(0, 1, n_steps)[:, np.newaxis] * dual_quat2
)
# renormalization (not required here because it will be done with conversion)
interpolated_dqs /= np.linalg.norm(interpolated_dqs[:, :4], axis=1)[:, np.newaxis]
interpolated_poses_from_dqs = ptr.transforms_from_dual_quaternions(interpolated_dqs)

Screw Linear Interpolation between Dual Quaternions

Dual quaternions also support screw linear interpolation (ScLERP) which is implemented with the dual quaternion power. The dual quaternion power uses the screw parameters of the pose difference to smoothly interpolate along the screw axis.

pose12pose2 = jt.compose_dual_quaternions(
    jt.dual_quaternion_quaternion_conjugate(dual_quat1), dual_quat2
)
exp_coords = jt.exponential_coordinates_from_dual_quaternion(pose12pose2)
offsets = jt.dual_quaternion_from_exponential_coordinates(
    exp_coords[np.newaxis] * np.linspace(0, 1, n_steps)[:, np.newaxis]
)
interpolated_poses_dq_slerp = ptr.transforms_from_dual_quaternions(
    jt.compose_dual_quaternions(
        np.array([np.asarray(dual_quat1) for _ in range(len(offsets))]), offsets
    )
)

Approximation: Linear Interpolation of Exponential Coordinates

A more crude approximation is the linear interpolation of exponential coordinates.

interpolated_ecs = (
    np.linspace(1, 0, n_steps)[:, np.newaxis] * exp_coords1
    + np.linspace(0, 1, n_steps)[:, np.newaxis] * exp_coords2
)
interpolates_poses_from_ecs = ptr.transforms_from_exponential_coordinates(
    interpolated_ecs
)

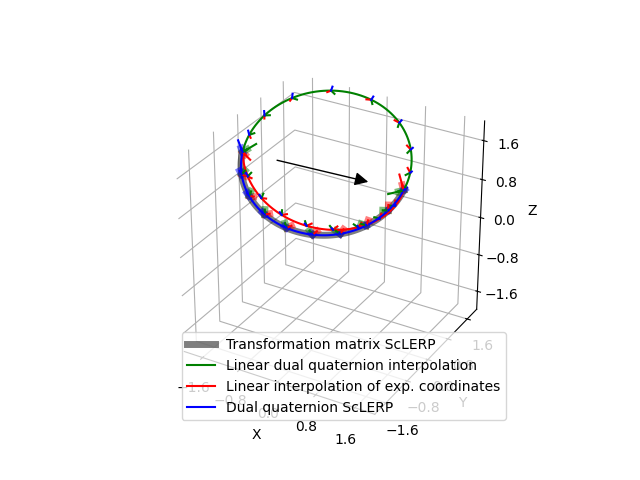
Plotting

We show all solutions in one 3D plot.

ax = pt.plot_transform(A2B=pose1, s=0.3, ax_s=2)
pt.plot_transform(A2B=pose2, s=0.3, ax=ax)
traj = ppu.Trajectory(
    interpolated_poses, s=0.1, c="k", lw=5, alpha=0.5, show_direction=True
)
traj.add_trajectory(ax)
traj_from_dqs = ppu.Trajectory(
    interpolated_poses_from_dqs, s=0.1, c="g", show_direction=False
)
traj_from_dqs.add_trajectory(ax)
traj_from_ecs = ppu.Trajectory(
    interpolates_poses_from_ecs, s=0.1, c="r", show_direction=False
)
traj_from_ecs.add_trajectory(ax)
traj_from_dqs_sclerp = ppu.Trajectory(
    interpolated_poses_dq_slerp, s=0.1, c="b", show_direction=False
)
traj_from_dqs_sclerp.add_trajectory(ax)
plt.legend(
    [
        traj.trajectory,
        traj_from_dqs.trajectory,
        traj_from_ecs.trajectory,
        traj_from_dqs_sclerp.trajectory,
    ],
    [
        "Transformation matrix ScLERP",
        "Linear dual quaternion interpolation",
        "Linear interpolation of exp. coordinates",
        "Dual quaternion ScLERP",
    ],
    loc="best",
)
plt.show()