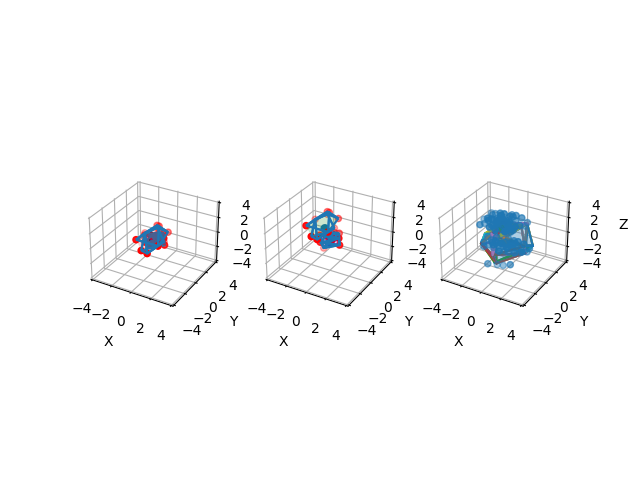
Collision resolution with EPA after GJK

[ 0.16013418 -0.31319129  0.0027869 ]
[-0.64738077  0.2573657   1.45919924]

print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
import pytransform3d.plot_utils as ppu
import pytransform3d.transformations as pt
from distance3d import random, plotting, gjk, epa, colliders, minkowski


random_state = np.random.RandomState(1)
mesh2origin, vertices, triangles = random.randn_convex(random_state, center_scale=0.0)
mesh2origin2, vertices2, triangles2 = random.randn_convex(random_state, center_scale=0.2)
points = pt.transform(mesh2origin, pt.vectors_to_points(vertices))[:, :3]
points2 = pt.transform(mesh2origin2, pt.vectors_to_points(vertices2))[:, :3]
collider1 = colliders.ConvexHullVertices(points)
collider2 = colliders.ConvexHullVertices(points2)
dist, p1, p2, simplex = gjk.gjk(collider1, collider2)
mtv, minkowski_faces, success = epa.epa(simplex, collider1, collider2)
assert success
assert all(p1 == p2)
print(p1)
print(mtv)

ax = ppu.make_3d_axis(ax_s=4, pos=131)
plotting.plot_convex(ax, mesh2origin, vertices, triangles, alpha=0.1)
plotting.plot_convex(ax, mesh2origin2, vertices2, triangles2, alpha=0.1, color="r")
ax.scatter(p1[0], p1[1], p1[2])
ppu.plot_vector(ax, p1, mtv)

ax = ppu.make_3d_axis(ax_s=4, pos=132)
plotting.plot_convex(ax, mesh2origin, vertices, triangles, alpha=0.1)
mesh2origin2[:3, 3] += mtv
plotting.plot_convex(ax, mesh2origin2, vertices2, triangles2, alpha=0.1, color="g")
plotting.plot_segment(ax, p1, p2 + mtv)

ax = ppu.make_3d_axis(ax_s=4, pos=133)
minkowski_points = minkowski.minkowski_sum(vertices, -vertices2)
ax.scatter(minkowski_points[:, 0], minkowski_points[:, 1], minkowski_points[:, 2])
plotting.plot_tetrahedron(ax, simplex)
for f in minkowski_faces:
    plotting.plot_triangle(ax, f[:3])
ax.scatter(0, 0, 0)
ax.scatter(mtv[0], mtv[1], mtv[2])

plt.show()