Learning Curves #2

Almost everyone working in the field of machine learning is usually pretty sure about what a learning curve is. It seems to be intuitive. The problem is that each field has its own typical definition of a learning curve and it is unusual to write it down explicitely. The only general definition that I found is in the first sentence of a section of a Wikipedia article. The rest of the paragraph does not even apply to everything any more. The essence is:

A learning curve is a plot relating performance to experience.

Machine Learning in General

For machine learning in general, the definition is quite clear: "A learning curve shows the validation and training score of an estimator for varying numbers of training samples." (scikit-learn documentation) Actually these are two learning curves. One that shows how well the optimization for the training data worked and one that tries to estimate the generalization error for varying number of training samples. The validation score is usually estimated with cross-validation. That is the reason why we can also plot the standard deviation interval for these curves. A score can be any performance metric that is applicable to the method and domain. An overview of the possible metrics can be found here. It includes metrics for classification (e.g. accuracy), clustering, and regression (e.g. mean squared error).

Here are some examples:


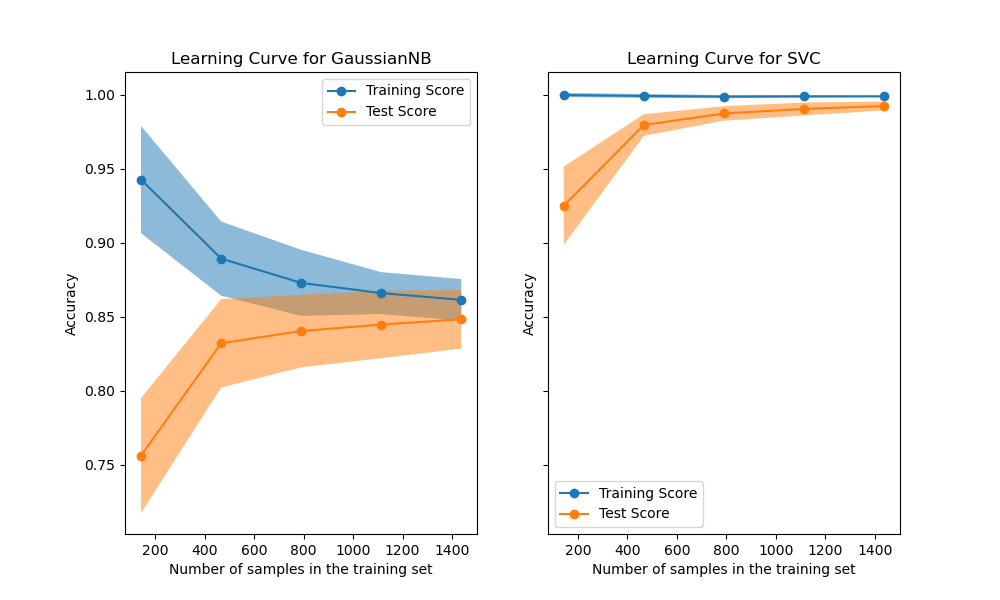
scikit-learn documentation, source.

In both cases the accuracy of classification algorithms is displayed. In the first example, you can clearly see that the algorithm poorly fits the training data. The model is not comlex enough. In the second example, the model fits the training data perfectly and even generalizes very well.

Neural Networks

In the neural networks (or deep learning) community, people usually have a different idea of a learning curve. Experience is typically not measured in samples. Experience is measured in optimization steps, that is, a neural network that has "seen" the same sample twice has more experience than a neural network that only saw it once. How we measure experience exactly is not so clear, however. There are numerous options:

Performance metrics are quite similar to those used for classification, regression, or to whatever is used in the domain in which the neural network is used. Often a learning curve just shows the loss, cost, or error that is optimized.

Because of the incremental and often expensive training of neural networks, cross validation is not an option for these learning curves. The standard procedure is to use a holdout validation set on which we can evaluate the neural network each time we want to compute a data point for the learning curve.

Here are some examples:

Reinforcement Learning

There is even more chaos in reinforcement learning (RL). It is not just unclear how to measure experience, there are even more ways to measure performance. It is often very specific to the domain in which we apply RL.

Let's start with experience. We have a classification that is very similar to the one for neural networks:

One thing to note is that there are multiple categories of algorithms: some methods learn after each step, some update after each episode and some only update after multiple episodes. That makes it sometimes quite hard to compare methods.

Measuring performance in RL is difficult because there are so many different approaches. In some publications you will find accumulated returns over all episodes, similar to the regret in multi-armed bandit problems. Sometimes only the return over episodes is shown. Sometimes an average return over multiple test episodes is shown. Sometimes the average return over multiple test episodes with different conditions is shown. Sometimes the return is called reward (return is the accumulated reward of an episode, in some problems only one reward is given at the end of an episode). Sometimes a cost is computed instead of a return. Sometimes domain-specific performance metrics are used. The list goes on and on.

Here are some examples: